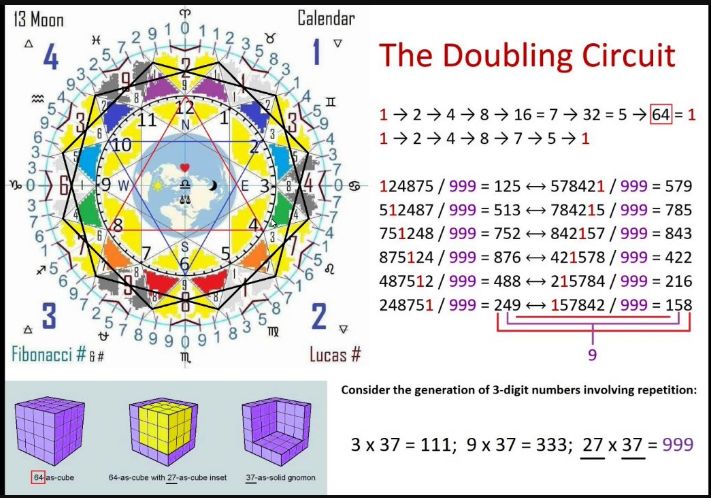
Phi Vortex Based Mathematics Torus Array
https://www.youtube.com/watch?v=1KS5XvP_rGI
“Phi Vortex Based Mathematics Torus Array” appears to be a concept that combines several mathematical and geometric principles:
1. Phi (φ): Phi, also known as the Golden Ratio or Divine Proportion, is a mathematical constant approximately equal to 1.618033988749895. It appears in various natural phenomena and is often associated with aesthetic beauty and harmonic proportions.
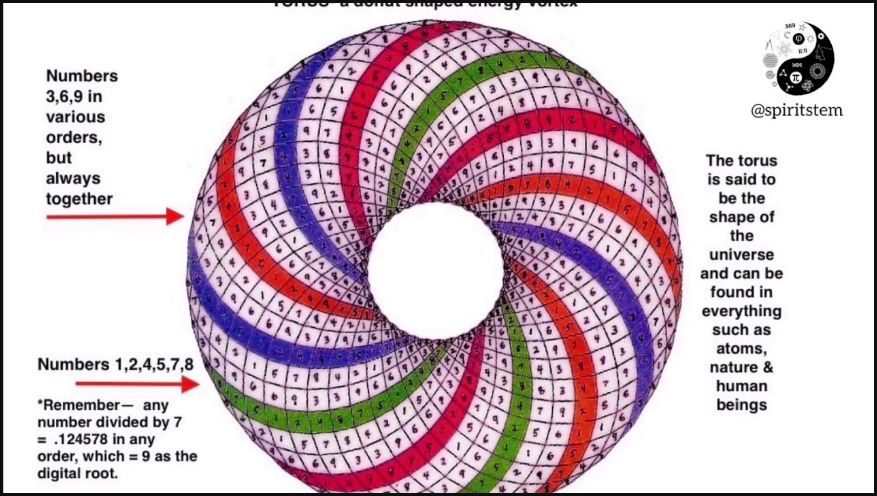
2. Vortex Based Mathematics (VBM): Vortex Based Mathematics is a theoretical framework proposed by Marko Rodin, which posits that numbers follow a pattern that can be visualized as a series of interconnected toroidal (donut-shaped) energy fields. VBM suggests that this pattern underlies the structure of the universe and has practical applications in fields such as energy generation and mathematics.
3. Torus: A torus is a three-dimensional geometric shape resembling a donut or a tire inner tube. It is characterized by a central hole surrounded by a continuous surface. Toroidal shapes are often used to represent energy flow and are found in various natural and man-made systems.
4. Array: An array refers to a systematic arrangement of objects or elements, often in rows and columns. In the context of “Phi Vortex Based Mathematics Torus Array,” it likely refers to a structured configuration of toroidal shapes based on the principles of Phi and VBM.
Combining these concepts, “Phi Vortex Based Mathematics Torus Array” may refer to a theoretical framework or visual representation that explores the interconnectedness of mathematical principles, geometric shapes, and energy dynamics within a toroidal array structure. It could be used to study patterns in mathematics, energy flow, or other phenomena related to the underlying structure of the universe, as theorized by proponents of Vortex Based Mathematics. However, it’s important to note that this concept may be speculative and theoretical, and its practical applications or scientific validity would require further investigation and empirical evidence.